Graph

Graph adalah jenis struktur data umum yang susunan datanya tidak berdekatan satu sama lain (non-linier). Graph terdiri dari kumpulan simpul berhingga untuk menyimpan data dan antara dua buah simpul terdapat hubungan saling keterkaitan.

Simpul pada graph disebut dengan verteks (V), sedangkan sisi yang menghubungkan antar verteks disebut edge (E). Pasangan (x,y) disebut sebagai edge, yang menyatakan bahwa simpul x terhubung ke simpul y.

Sebagai contoh, terdapat graph seperti berikut:

Graph di atas terdiri atas 4 buah verteks dan 4 pasang sisi atau edge. Dengan verteks disimbolkan sebagai V, edge dilambangkan E, dan graph disimbolkan G, ilustrasi di atas dapat ditulis dalam notasi berikut:

V = {0, 1, 2, 3}

E = {(0,1), (0,2), (0,3), (1,2)}

G = {V, E}

Graph banyak dimanfaatkan untuk menyelesaikan masalah dalam kehidupan nyata, dimana masalah tersebut perlu direpresentasikan atau diimajinasikan seperti sebuah jaringan. Contohnya adalah jejaring sosial (seperti Facebook, Instagram, LinkedIn, dkk)

Pengguna di Facebook dapat dimisalkan sebagai sebuah simpul atau verteks, sementara hubungan pertemanan antara pengguna tersebut dengan pengguna lain direpresentasikan sebagai edge. Tiap tiap verteks dapat berupa struktur yang mengandung informasi seperti id user, nama, gender, dll.

Tidak hanya data pengguna, data apapun yang ada di Facebook adalah sebuah simpul atau verteks.Termasuk foto, album, komentar, event, group, story, dll.

Pengguna dapat mengunggah foto. Ketika telah diunggah, foto akan menjadi bagian dari album. Foto juga dapat dikomentari oleh pengguna lain dan mereka dapat saling berbalas komentar.

Semuanya terhubung satu sama lain, baik dalam bentuk relasi one-to-many, many-to-one, atau many-to-many.

Jenis-jenis Graph

Graph dapat dibedakan berdasarkan arah jelajahnya dan ada tidaknya label bobot pada relasinya.

Berdasarkan arah jelajahnya graph dibagi menjadi Undirected graph dan Directed graph.

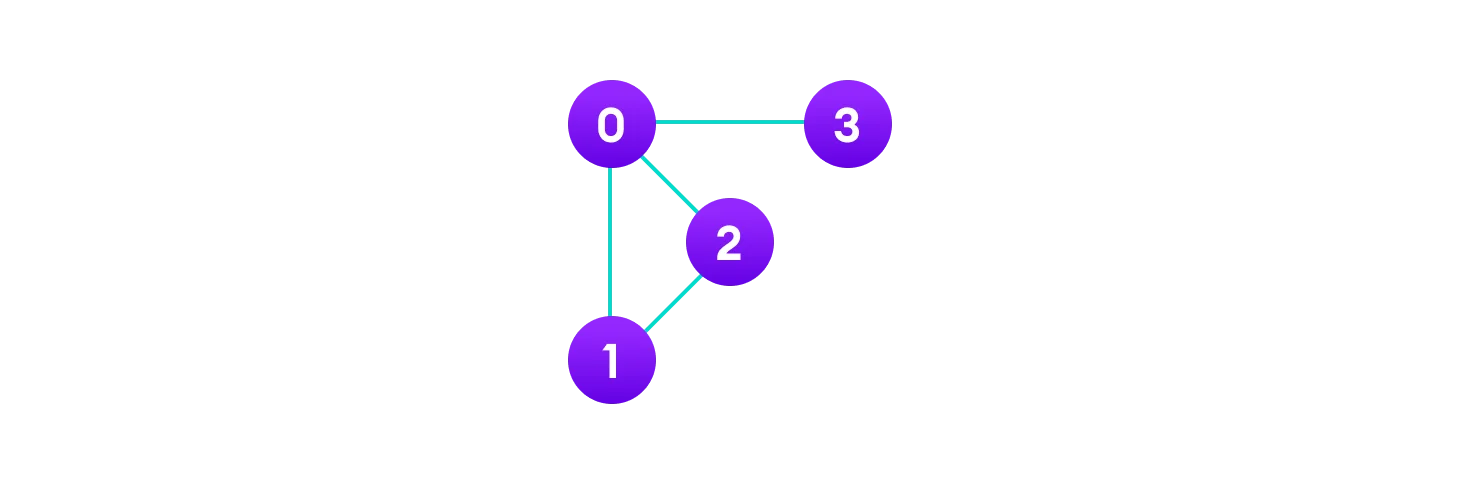
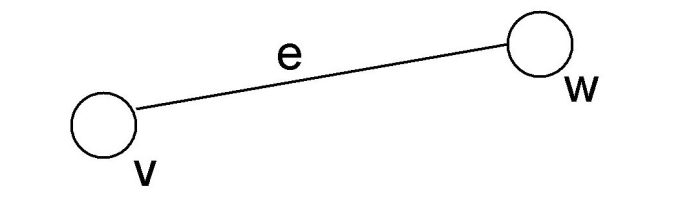
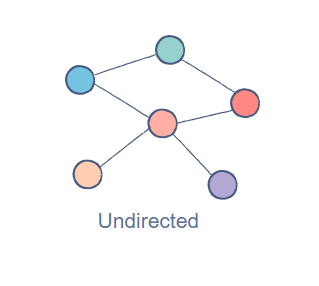
Undirected Graph

Pada undirected graph, simpul-simpulnya terhubung dengan edge yang sifatnya dua arah. Misalnya kita punya simpul 1 dan 2 yang saling terhubung, kita bisa menjelajah dari simpul 1 ke simpul 2, begitu juga sebaliknya.

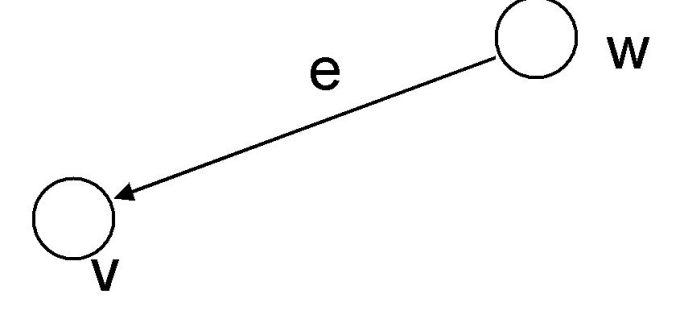
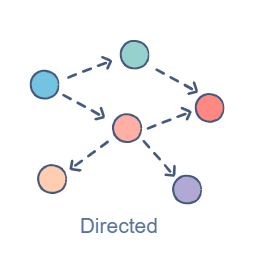
Directed Graph

Kebalikan dari undirected graph, pada graph jenis ini simpul-simpulnya terhubung oleh edge yang hanya bisa melakukan jelajah satu arah pada simpul yang ditunjuk. Sebagai contoh jika ada simpul A yang terhubung ke simpul B, namun arah panahnya menuju simpul B, maka kita hanya bisa melakukan jelajah (traversing) dari simpul A ke simpul B, dan tidak berlaku sebaliknya.

Selain arah jelajahnya, graph dapat dibagi menjadi 2 berdasarkan ada tidaknya label bobot pada koneksinya, yaitu weighted graph dan unweighted graph.

Weighted Graph

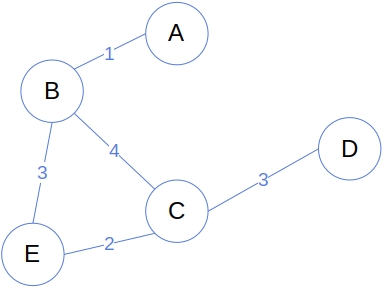
Weighted graph adalah jenis graph yang cabangnya diberi label bobot berupa bilangan numerik. Pemberian label bobot pada edge biasanya digunakan untuk memudahkan algoritma dalam menyelesaikan masalah.

Contoh implementasinya misalkan kita ingin menyelesaikan masalah dalam mencari rute terpendek dari lokasi A ke lokasi D, namun kita juga dituntut untuk mempertimbangkan kepadatan lalu lintas, panjang jalan dll. Untuk masalah seperti ini, kita bisa mengasosiasikan sebuah edge e dengan bobot w(e) berupa bilangan ril.

Nilai bobot ini bisa apa saja yang relevan untuk masalah yang dihadapi: misalnya jarak, kepadatan, durasi, biaya, probabilitas, dan sebagainya.

Unweighted Graph

Berbeda dengan jenis sebelumnya, unweighted graph tidak memiliki properti bobot pada koneksinya. Graph ini hanya mempertimbangkan apakah dua node saling terhubung atau tidak.

Karakteristik Graph

Graph memiliki beberapa karakteristik sebagai berikut:

Jarak maksimum dari sebuah simpul ke semua simpul lainnya dianggap sebagai eksentrisitas dari simpul tersebut.
Titik yang memiliki eksentrisitas minimum dianggap sebagai titik pusat dari graph.
Nilai eksentrisitas minimum dari semua simpul dianggap sebagai jari-jari dari graph terhubung.

Fungsi dan Kegunaan Graph

Fungsi dan kegunaan graph di antaranya:

Graph digunakan untuk merepresentasikan aliran komputasi.
Digunakan dalam pemodelan grafik.
Graph dipakai pada sistem operasi untuk alokasi sumber daya.
Google maps menggunakan graph untuk menemukan rute terpendek.
Graph digunakan dalam sistem penerbangan untuk optimasi rute yang efektif.
Pada state-transition diagram, graph digunakan untuk mewakili state dan transisinya.
Di sirkuit, graph dapat digunakan untuk mewakili titik sirkuit sebagai node dan kabel sebagai edge.
Graph digunakan dalam memecahkan teka-teki dengan hanya satu solusi, seperti labirin.
Graph digunakan dalam jaringan komputer untuk aplikasi Peer to peer (P2P).
Umumnya graph dalam bentuk DAG (Directed acyclic graph) digunakan sebagai alternatif blockchain untuk cryptocurrency. Misalnya crypto seperti IOTA

Kelebihan Graph

Keunggulan dari struktur data graph adalah sbb:

Dengan menggunakan graph kita dapat dengan mudah menemukan jalur terpendek dan tetangga dari node
Graph digunakan untuk mengimplementasikan algoritma seperti DFS dan BFS.
Graph membantu dalam mengatur data.
Karena strukturnya yang non-linier, membantu dalam memahami masalah yang kompleks dan visualisasinya.

Kekurangan Graphh

Adapun kekurangan dari struktur data graph di antaranya

Graph menggunakan banyak pointer yang bisa rumit untuk ditangani.
Memiliki kompleksitas memori yang besar.
Jika graph direpresentasikan dengan adjacency matrix maka edge tidak memungkinkan untuk sejajar dan operasi perkalian graph juga sulit dilakukan.

Istilah-istilah pada Graph

Incident, Jika e merupakan busur dengan simpul-simpulnya adalah v dan w yang ditulis e=(v,w), maka v dan w disebut “terletak” pada e, dan e disebut incident dengan v dan w.
egree (derajat), indegree dan outdegree, Degree sebuah simpul adalah jumlah busur yang incident dengan simpul tersebut.
- Indegree sebuah simpul pada graph berarah adalah jumlah busur yang kepalanya incident dengan simpul tersebut, atau jumlah busur yang “masuk” atau menuju simpul tersebut.
- Outdegree sebuah simpul pada graph berarah adalah jumlah busur yang ekornya incident dengan simpul tersebut, atau jumlah busur yang “keluar” atau berasal dari simpul tersebut.
pada graph tidah berarah, 2 buah simpul disebut adjacent bila ada busur yang menghubungkan kedua simpul tersebut. Simpul v dan w disebut adjacent.

Pada graph berarah, simpul v disebut adjacent dengan simpul w bila ada busur dari w ke v.
Successor dan Predecessor

Pada graph berarah, bila simpul v adjacent dengan simpul w, maka simpul v adalah successor simpul w, dan simpul w adalah predecessor dari simpul v

Path

Sebuah path adalah serangkaian simpul-simpul yang berbeda, yang adjacent secara berturut-turut dari simpul satu ke simpul berikutnya.

Tree VS Graph

spanning tree

Spanning tree adalah sebuah subgraf yang terdiri dari simpul-simpul yang sama dengan graf asli, tetapi hanya mengandung sisi-sisi yang membentuk sebuah pohon. Dalam sebuah pohon, tidak ada sirkuit (lintasan tertutup) dan setiap simpul dapat dijangkau dari simpul lainnya melalui tepat satu jalur. Sebuah graf tak terarah bisa memiliki lebih dari satu spanning tree.

Minimum Spanning Tree

Pohon rentang minimum atau pohon rentang berbobot minimum (bahasa Inggris: minimum spanning tree, MST) adalah himpunan bagian dari himpunan garis-garis (edge) suatu graf berbobot tak berarah yang menghubungkan semua titik tanpa membentuk siklus dan dengan total bobot minimum. Dengan kata lain, ini adalah pohon rentang yang total bobotnya minimum.

Ada beberapa kasus yang menggunakan pohon rentang minimum. Misalnya, perusahaan telepon mencoba untuk menghubungkan telepon-telepon rumah dengan kabel sehingga kabel yang dipakai sependek mungkin. Di beberapa tempat, mungkin dibutuhkan penggalian sehingga biayanya bertambah. Dengan kata lain, "bobot" garisnya bertambah. Satuan yang biasa dipakai dalam permasalahan ini adalah biaya (cost). Dalam konteks ini, pohon rentang minimum adalah jalur yang menggunakan kabel sependek mungkin atau dengan biaya serendah mungkin.

Algoritme Dijkstra,

Algoritma Dijkstra pertama kali ditemukan oleh seorang ilmuwan komputer bernama Edsger W. Dijkstra pada tahun 1956. Algoritma ini awalnya diterbitkan dalam paper berjudul “A Note on Two Problems in Connexion with Graphs” pada tahun 1959.

Sejak saat itu, algoritma Dijkstra telah menjadi salah satu algoritma yang paling banyak digunakan untuk mencari jalur terpendek dalam berbagai aplikasi, termasuk navigasi, optimasi jaringan, dan perencanaan rute.

Dengan penemuan algoritma Dijkstra, Edsger W. Dijkstra juga menjadi dikenal sebagai salah satu tokoh utama dalam bidang ilmu komputer dan kontribusinya yang besar dalam pengembangan ilmu komputer dan teori graf.

Algoritma Dijkstra adalah algoritma yang digunakan untuk mencari jalur terpendek dari satu titik ke semua titik lain dalam sebuah graf berbobot.

Dijkstra mengembangkan algoritma ini untuk menemukan jalur terpendek dalam sistem transportasi dengan menggunakan bobot sebagai representasi jarak antar kota.

Sejak penemuan algoritma ini, Dijkstra diakui sebagai salah satu kontributor terbesar dalam bidang komputer dan matematika.

Cara Kerja Algoritma Dijkstra

inisialisasi
Mulai dengan graf berbobot yang terdiri dari simpul-simpul (node) dan sisi-sisi (edge) yang menghubungkan simpul-simpul tersebut. Setiap sisi memiliki bobot yang menyatakan jarak atau biaya antara dua simpul yang terhubung. Selain itu, inisialisasi juga melibatkan penentuan simpul awal (sumber) dari mana algoritma akan memulai mencari jalur terpendek
Tentukan Jarak Awal
Setiap simpul dalam graf diinisialisasi dengan nilai jarak tak terhingga (infinity), kecuali untuk simpul awal yang diinisialisasi dengan nilai nol. Dalam langkah ini, algoritma juga menyimpan catatan jalur yang telah ditemukan dari simpul awal ke simpul lain.
Pilih Simpul dengan Jarak Terdekat:
Algoritma Dijkstra berjalan secara iteratif. Pada setiap iterasi, algoritma mencari simpul dengan jarak terpendek yang belum dikunjungi. Pencarian simpul dilakukan dengan membandingkan nilai jarak saat ini dari simpul-simpul yang belum dikunjungi.
Perbarui Jarak Simpul Terhubung:
Setelah simpul dengan jarak terdekat dipilih, algoritma memeriksa semua simpul yang terhubung langsung dengan simpul tersebut. Untuk setiap simpul terhubung yang belum dikunjungi, algoritma membandingkan jarak saat ini dengan jarak baru yang dihitung melalui simpul terdekat tadi. Jika jarak baru lebih kecil dari jarak saat ini, maka jarak saat ini diperbarui dengan jarak baru. Selain itu, catatan jalur juga diperbarui sesuai dengan jalur baru yang ditemukan.
Tandai Simpul Terdekat:
Setelah pembaruan jarak dan jalur dilakukan, simpul yang sudah dikunjungi ditandai sehingga tidak akan dipertimbangkan lagi pada iterasi berikutnya.
Ulangi Langkah 3 hingga 5
Langkah-langkah 3 hingga 5 diulangi hingga seluruh simpul dalam graf telah dikunjungi. Pada setiap iterasi, algoritma memilih simpul dengan jarak terdekat yang belum dikunjungi untuk dianalisis. Proses ini berlanjut hingga algoritma telah menemukan jalur terpendek dari simpul awal ke semua simpul lain dalam graf.
Hasil Akhir:
Setelah seluruh simpul telah dikunjungi dan jarak terpendek telah dihitung, algoritma Dijkstra menghasilkan catatan jalur terpendek dari simpul awal ke simpul-simpul lain dalam graf. Dengan demikian, algoritma ini berhasil menyelesaikan pencarian jalur terpendek.

Pengertian Algoritma Kruskal

Algoritma Kruskal pertama kali dipopulaerkan oleh Joseph Kruskal pada tahun 1956. Algoritma Kruskal adalah sebuah algoritma dalam teori graf yang mencari sebuah Minimum Sanning Tree untuk sebuah graf berbobot yang terhubung. Ini berarti mencari subset dari sisi yang membentuk sebuah Tree yang menampung setiap vertex, dimana total bobot dari semua sisidalam Tree adalah minimum. Jika graf tidak terhubung, kemudian ini mencari sebuah Minimum Spanning Forest (sebuah Minimum Spanning Tree untuk tiap komponen yang terhubung ). Algoritma Kruskal adalah suatu contoh dari Algoritma Greedy.

synatyc

Home

Profile

Data Book